作者：老喻在加@来源：孤独大脑

开始

遥远的外星球上，机器人公主不可救药地迷恋上了传说中的人类。

于是，机器人王子为了追求公主，在身上抹满黏糊糊的东西，冒充人类去接受公主的残酷盘问。

在经过几轮低劣的伪装之后，王子迎来了一个比较复杂的问题：

“姆亚姆拉克，告诉我，你们白人是怎么建造后代的？”

“我们不建造后代。”

王子继续回答：

“我们基于马尔可夫随机过程理论，通过统计学的方法进行程序编写，也就是说，这带有很大的概率性和偶然性。”

这篇名为《费勒茨王子与水晶公主》的小说的作者，是被誉为“科幻届的博尔赫斯”的莱姆。

在半个世纪前的文字，莱姆用“马尔可夫随机过程理论”来描述人类的繁衍（包括此前充满随机性的交配行为），这真有趣。

在概率论及统计学中，马尔可夫过程（英语：Markov process）是一个具备了马尔可夫性质的随机过程，因为俄国数学家安德雷·马尔可夫得名。

马尔可夫过程是不具备记忆特质的。

换言之，马尔可夫过程的条件概率仅仅与系统的当前状态相关，而与它的过去历史或未来状态，都是独立、不相关的。

安德雷·马尔可夫自己可能也没预测到，自己的这个看起来有点儿奇怪的概念，在100年后竟会发挥如此神奇的力量，例如：

• 语音识别系统的基础；

• 文艺复兴基金的赚钱模型；

• 谷歌所使用的网页排序算法；

......

本文围绕“无记忆”展开：

真正的高手，擅长打无记忆的牌。

一

具备离散状态的马尔可夫过程，通常被称为马尔可夫链。

马尔可夫链，为状态空间中经过从一个状态到另一个状态的转换的随机过程。

该过程要求具备“无记忆”的性质：下一状态的概率分布只能由当前状态决定，在时间序列中它前面的事件均与之无关。

假如一个街上，有两家奶茶店：A和B。

• A奶茶店的顾客，在喝了奶茶之后，有70%的人会继续选择该店，有30%会选择去B奶茶店；

• B奶茶店的顾客，在喝了奶茶之后，有90%的人会继续选择该店，有10%会选择去A奶茶店。

假如一开始的时候，A和B的顾客是一样多的，例如都是500个，请问经过一段时间后，两家的顾客分别是多少？

答案是：A店有250个顾客，B店有750个顾客。

我们变换一下条件。假如一开始的时候，这条街只有A一家奶茶店，1000个顾客全是A的。而B刚刚开张，1个顾客都没有。请问经过一段时间后，两家的顾客分别是多少？

答案还是：A店有250个顾客，B店有750个顾客。

如你所知，这是一个马尔可夫链的统计均衡。

你可能会说，我喝了好久A了，喝出感情了，怎么能说和此前无关呢？

不管你对A的感情分有多高，也都被时光沉淀到你当下这杯奶茶的体验当中了。所以，你的下一次选择，依然只取决于你这一次喝奶茶的体验。

这种特定类型的“无记忆性”称作马尔可夫性质。

在马尔可夫链的每一步，系统根据概率分布，可以从一个状态变到另一个状态，也可以保持当前状态。

状态的改变叫做转移，与不同的状态改变相关的概率叫做转移概率。

我画一下奶茶店的转移概率：

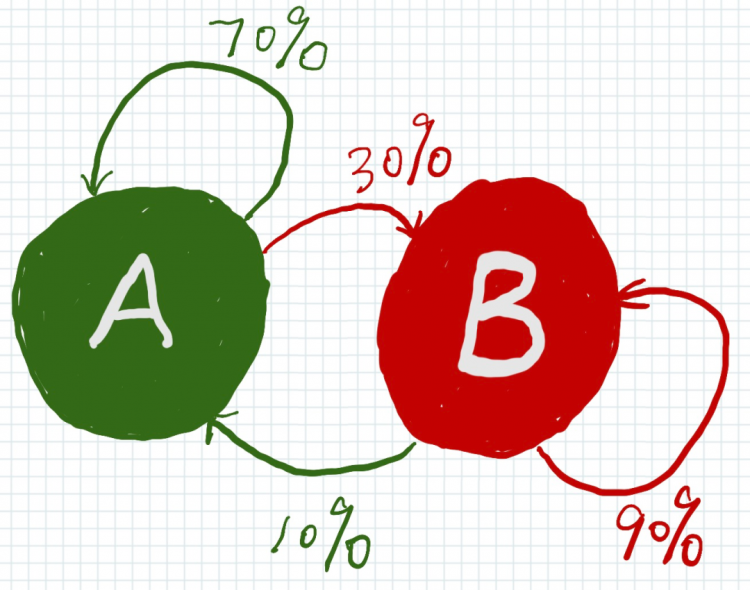
如上，箭头指向自己的，是指客户留存。指向别人，则是客户流失。

马尔可夫模型的一个特点是：当转移概率固定时，不管初始数是多少，总会达到一个“命中注定”的、唯一的统计均衡。

所以，即使奶茶店B刚开张，一个顾客也没有，要不了多久，也会抢走大部分奶茶店A的顾客。

不管A开始的时候多么有优势，钱最后还是追着B去了。

二

一种对于命运的数字隐喻是“大数定律”。

我在《人生算法》这本书里也说过，一个骰子扔出某个数字的概率，取决于自身的结构，与手法和努力无关。

但是，大数定律里的抛硬币游戏，需要每一次抛硬币都是完全独立的。

而数学家帕维尔·涅克拉索夫则认为：现实世界中的事物是相互依存的（比如人的行为），所以现实中的事物并不恰好符合数学模式或分布。

马尔可夫不这么认为。他建立了一个模型，在这个模型中，结果的概率取决于以前发生的事件，但长期来看仍然遵循大数定律。

如雪莱所说：历史是一部循环诗，由时间写在人的记忆上。

《天才与算法》里写道：

抛硬币的结果并不取决于以前抛硬币的结果，所以这不是马尔可夫理想的模型。

但是，如果增加一点依赖关系，使下一个事件取决于刚刚发生了什么，而不是整个系统如何影响了当前事件，又会怎么样呢？

每个事件的概率仅取决于先前事件的一系列事件被称为马尔可夫链。

预测天气就是一个例子：明天的天气肯定取决于今天的天气，但并不特别依赖于上周的天气。

由此，我们结合奶茶店的例子，可以发现马尔可夫链“宿命论”般的特点：

1、历史是无关紧要的，你再百年老店也没用；

2、初始条件是无关紧要的，你再高市场占有率也没用；

3、各种折腾也是没用的。你再营销，再数字化，做各种视频拉来流量，都无法改变宿命般的统计均衡，然后保持不变。

当然，即使马尔可夫链很强大，用自然科学解释社会科学，依然有各种各样的假设和约束。

在此，我们暂时略过。

《模型思维》一书总结道：

• 在应用马尔可夫模型解释现象或预测趋势时，建模者对状态的选择至关重要。状态的选择决定了这些状态之间的转移概率。

• 假如不改变转移概率，那些试图通过为期只有一两天的活动来激发学生学习兴趣的做法，可能不会产生什么有意义的影响。与此类似，进入社区“送温暖”、来到公园“捡垃圾”的志愿者，一次性的资金涌入，无论其规模大小，影响都会消失。

同理，以上观点，也是基于动态系统都满足马尔可夫模型的假设。在假设之外，历史、干预、事件仍可能产生长期影响。

三

现在，来到本文的重点：

马尔可夫过程的无记忆性。

让我们先忘掉马尔可夫，只说说“无记忆”。

没人知道文艺复兴基金的算法黑盒子里是如何运用隐马尔可夫链的，不如我们先研究一下人肉的“无记忆”。

李录被芒格视为“房间里最聪明的人”，是价值投资的信徒，毋庸置疑是位长期主义者，可是他又说投资人应该像个高尔夫球手，应该打无记忆的球。他说：

我有个投资做得非常好的朋友跟我说投资和打高尔夫球很像，我很同意。你必须得保持平常心，你的心绪稍稍一激动，肯定就打差了。

前一杆跟后一杆没有一点关系，每一杆都是独立的，前面你打了一个小鸟球，下一杆也不一定能打好。而且每一杆都要想好风险和回报。

一个洞的好坏胜负并不会决定全局，直到你退役之前，都不是结果。而你留在身后的记录就是你一生最真实的成绩，时间越长，越不容易。

所以多打打高尔夫球，对于培养投资人的品性有帮助。

如上所述，其实也是老生常谈了，几乎每个做投资或者做投机的，或者玩儿德州扑克的，或者跟着AI学围棋的，都会懂得“无记忆”的含义。

那么，“无记忆”就是指一个人要在竞技和下注中保持冷静吗？

没错，这一点的确很重要。

在德州扑克的游戏过程当中，被对方几个OUTS的BADBEAT，这其实很正常的，波动就是德州扑克（包括别的随机性游戏）的天然属性。

绝大多数人会在这种波动中晕船，以致情绪失控。

扑克中的术语叫“上头”，比如坐在牌桌上，每当系统风险给你带来不利的时候你的情绪会失控，会开始胡乱地加注入池、胡乱地诈底或者买一些不该买的牌。

（以上关于德扑的文字，是我从一篇抄我的文章里抄回来的。）

投资上也是如此，很多人掉进坑里，会更加卖力地挥动铲子，越挖越深。

所以，这个时候，打“无记忆”的牌，就会格外重要。

不要因为糟糕的结果而否定正确的选择。

在现实中，你坚持做正确的事情，短期内未必有很好的回报，但你还是要坚持做正确的事情。

然而，打“无记忆”的牌，绝非控制自己的情绪这么简单。

四

我将打“无记忆”的牌，分为如下5个层次：

第一层次：当下的无记忆。

控制情绪，保持平常心。

第二层次：过往的无记忆。

理性对待沉没成本。

第三层次：决策的无记忆。

重新构建决策点。

第四层次：已知的无记忆。

压缩过往，“鸟瞰”自己的已知条件。

第五层次：人设的无记忆。

不要为了人设、为了维护自我干蠢事。

1

第一层次：当下的无记忆

控制情绪，保持平常心。上一段已经说过了。

2

第二层次：过往的无记忆

理性对待沉没成本。

这方面的说法和案例也很多了。

研究行为经济学的卡尼曼和塞勒，对此都有很深刻的研究，可以去找他们的书看。

段永平讲过一个小故事，可能是很多人在生活中都会干的蠢事：

我在美国的时候，去机场接一位步步高的同事，估计要在机场等一个小时，所以在机场停车场投了一个小时停车收费的币，结果，那位同事提前半小时就来了。

这就有个问题：多投了半个小时的币，是继续在车里等这半小时，还是浪费多投的这半小时的钱？结论不言而喻的，肯定是开车走人。

段永平想表达的是：

所以，忘掉你多扔的停车费吧，忘掉你的沉没成本，忘掉你的股票成本，股票自己是没有记忆的。

3

第三层次：决策的无记忆

你应该重新构建决策点。

当你需要做决策的时候，你要像一个外来者，或者像一个外星人。

例如，假如你不是一个创业者，而是一个派来接管你的创业公司的人，你还会做自己正在做的事情吗？

有些人会说，我就是因为已经做了，所以必须有个交代。假如我是外来者，就没有这个道德压力了，自然会理性一些。

好吧，也许这也是创业者的优势之一，然而，即使是死磕到底，也可以有更聪明的方法。至少对投资人而言，他要的是你赚得光荣，而非“死的伟大”。

假设自己是个外来者，其实是人为设置一个决策点。

作为决策者，你应该为未来负责，而不是为过去解释。

我曾经写过，厉害的人都是人肉阿尔法狗。

什么叫人肉阿尔法狗？

先看阿尔法狗如何做决策。

阿尔法狗几乎会在每一手棋时，都计算自己的赢棋概率。

即：对它而言，每一个决策点都是独立的，阿尔法狗都会冷静地寻找“当下”的最大获胜概率。

所以，AI下棋，特别擅长于脱先，绝不纠缠，哪里价值大就下在哪里。

首先是目标的连续性，然后是策略的连续性，最后是动作的连续性。

然而，人类为了表面上连续性，可以踩着西瓜皮滑到任何地方。

所谓的无记忆，就是客观冷静地审视当下整体局面：

• 对的事情要坚持，忘掉前一秒的鼻青脸肿；

• 不对的事情，不管付出多大的代价都不做，都要叫停。

如何区分“对”还是“不对”？

这就是人生的难题和乐趣所在了，必须由每个人自己来回答。

4

第四层次：已知的无记忆

压缩过往，“鸟瞰”自己的已知条件。

要理解这一点，还是用围棋来类比。

围棋有一点特别奇怪的地方。

围棋是与顺序有关的游戏。

• 围棋棋子除了颜色以外，完全一样，不像象棋那样分帅车兵马。

• 另外，围棋的棋子，落下之后就不能移动。

• 围棋棋子的效率和价值，是由棋子之间的空间关系而决定的。

• 就像搭宜家家具或者乐高玩具，即使空间位置对了，但如果顺序错了，也不行。

可是，对于一局棋的过去而言，“顺序”并不重要。这就是“奇怪”的地方。

这方面最有趣的概念，是围棋里的“手割”，但今天我不想展开了。

让我略去围棋关于时空的思考过程，来概述一下：

当我们站在围棋对局中的某个决策点上，当下的局面，是所有“已知”构建的一个静态空间结构图，单个棋子当初的使命、顺序，并不能作为决策的依据。

你要忘掉过往的假设，过往的因果，这并非完全抛弃存量，而是压缩过去，将其作为当下决策的已知条件，而非约束条件。

这里面的无记忆，还体现在一流的决策者不会受限于自己是否真的拥有那些资源。

我年少时学下围棋，最大的收获就是学会思考：

• 假如这里我能够连续走两手，会有什么结果？

• 假如我这里再多一个子，我就会有什么样的手段？

这是另外一种更高级别的无记忆，如王兴所说：

5

第五层次：人设的无记忆

不要为了人设，为了维护自我，而去干蠢事。

忘掉自己的人设，这可能是“无记忆”最艰难的地方。

因为反人性。

这里的“人设的无记忆”，当然不是指厚黑学。

这方面的各种鸡汤文够多了，我且略过。

想和你分享一个我记忆深刻的故事：

2004年10月，乔布斯有机会见到了自己心目中的偶像鲍勃·迪伦。

狂人乔布斯格外紧张，不仅因为鲍勃是他心目中的英雄之一，还因为他担心：

万一他本人不像我想象中那么聪明？

或者，他只是在“模仿”自己？就像很多人那样。

绝大多数人都是在“模仿”自己：

• 失意者通过自己的糟糕记忆重复自己；

• “成功者”通过幻觉强化自己的一贯正确。

别模仿昨天，未来学家彼得·伊利亚德说：

“今天我们如果不生活在未来，那么未来我们将生活在过去”。

忘掉自己的人设吧，因为根本没人在意。

最后

时间给了我们一种奇怪的幻觉：

• 过去如何被堆积起来（并被记忆自由重组）？

• 现在如何存在而又不存在？

• 未来如何总是给人以期待？

人有一种神奇的天赋，那就是对未来的幻想。动物似乎并不具备这一点。

往前看，打无记忆的牌，是一种高级的策略，更是一种伟大哲学。

你需要智慧，还需要司汤达所描述的勇气：

向前看，是我们唯一的选择。

对于那些仍然相信未来的人，请允许我与你分享一首名为《每一粒微沙》的歌。

这是乔布斯最喜欢的鲍勃·迪伦的歌。

在两人唯一的那次见面时，乔布斯很开心地发现，自己的偶像并不是在“模仿迪伦他自己”。

据说这首歌是关于“放下一切、祈祷救赎”。

其中有段歌词如下：

不要存心回首任何错误，像该隐知耻

我开始注视这些必须甩掉的陈年旧事

在愤恨的当下

我能看见造物主之手

在每片颤动的叶里，

在每粒微沙之中

百万读者都在读

【悦享新年】FMBA奇妙书单（附链接）

2021，每个人都了不起

吴晓波：未来十年，我们所认为的能力将荡然无存

中国宏观展望：2021

史上最严退市新规正式落地

人间真实！北京，全国最早醒来的城市…

秦朔：创新何太急

这场病毒放大器

人最大的本事，就是靠谱

财政到底有多紧？

负利率时代的泡沫、掠夺和危机！

全球货币再宽松：一次无法降落的飞行

美国人眼中的中国崛起 | 哈佛教授TED演讲

中国最赚钱的公司，要开始去库存了！

成年人的崩溃，都是静悄悄：你能挺过多少坎，就能成多大事

为什么有的人年纪轻轻，思想深度却远高于常人？

杠杆的轮回，众生的焦虑

50句惊艳世人的电影台词：请原谅我戳痛了你所有记忆

由FMBA历届校友推荐的文章集锦，版权属于原作者