点击蓝色字关注我们哟！

01

不算内行的“数学家”

大学里有棵树，名字叫“高数”，上面挂了很多人。树下有座坟，名叫微积分……很多人想起高数估计还有被支配的恐惧，对于没有天分的人来讲，数学就像一个黑洞，无论投入多少能量都会被它吸光。

几年前，我曾在某乎上回答了一个关于数学的问题，获得一些赞同之后，俨然成为了一个名不符实的“数学家”，像什么磨光函数、飘带函数、欧拉角……各种我连名字都没听过的数学问题都来邀请我回答。

呃……人家也是个数学小白啊，只是用到哪学到哪。这不，学习“管理经济学”的时候又要用到那棵树了，温故知新的同时，来顺道祭奠一下微积分吧。

02

一起聊聊：什么是边际？

我们在日常生活中经常听到有人讲“边际成本”、“边际收益“这样的经济学词汇，往往左耳朵进右耳朵出，并不知道真正的含义。

未接触管理经济学之前，我也一脸问号。什么是边际？我们平时在生产或生活中只讲“成本”、“收益”好像也够用了啊，经济学家们为什么要发明“边际”这个词？

学习之后，惊讶地发现“边际”是经济学中极其重要的思考问题的方式。

我们知道管理经济学是企业视角的微观经济学，其分析问题的出发点是最优化，追求高效率、高收益和高效益。而经济学分析问题的核心思想就是：增量分析。

也许就是因为需要把聚光灯打在“增量”上，对增量进行定量的分析，才引入“边际”这个概念吧。从某种意义上来看，“边际”就是“增量”变化后引发的变化，即当一个因素改变一个单位时，受其影响的另一经济指标发生的变化。

比如边际成本就是指新增一单位生产商品所带来的成本增量，而边际收益则是指增加一单位产品的销售所增加的收益。

“边际”这个概念可以应用到很多地方，我们来举个例子。假设下表是一家工厂生产某种商品雇佣不同数目的工人所带来的产量变化。

工人人数 （L））	总产量 （Q）	平均产量 （AP）	边际产量 （MP）
		——
1	2	2	2
2	5	2.5	3
3	9	3	4
4	14	3.5	5
5	22	4.4	8
6	40	6.7	18
7	57	8.1	17
8	63	7.9	6
9	64	7.1	1
10	63	6.3	-1

如表中所示，如果只有一个工人工作，商品的总产量是2个，如果增加一个工人变成2个人，那么由于工人之间可以互补，总产量就可以增加到5个。因为增加这个工人就多生产了3个，那么因为增加这1个工人（单位工人）而引起的产量的变化我们就可以称之为“边际产量”。

那么我们为什么要去研究这个“边际”问题呢？我们从表中可以看出，对前6名工人来说，边际产量是随工人人数的增加而增加的。但再增加工人，边际产量就会递减。到第10名工人时甚至会使总产量下降，边际产量已经小于0变为负值，说明该厂的工人已经太多，也许工人之间已经互相妨碍，说明此时雇佣10名工人已经无法促进反而阻碍了高效率的生产。

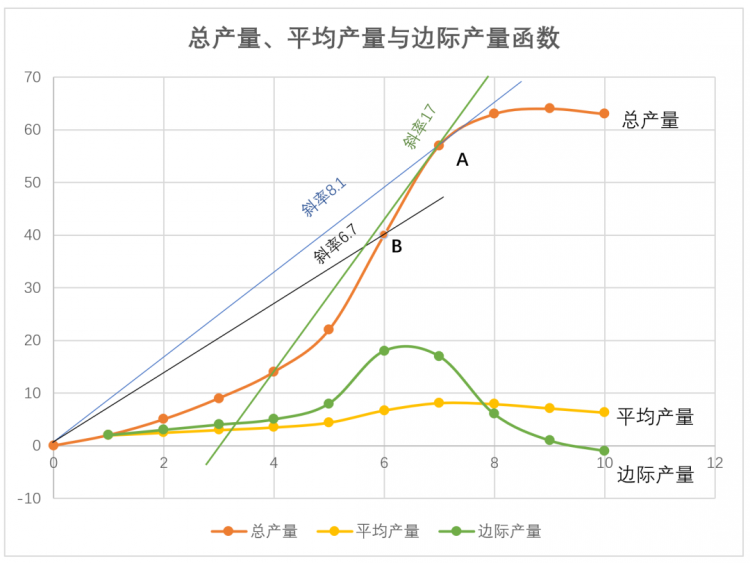
一图胜千言，我们把上表中的数值画在坐标轴里，然后连接起来就形成了三条函数曲线，分别对总产量、平均产量和边际产量进行函数示意。

那么了解边际这一概念的意义就显现出来了，我们可以看出当边际产量为正值时，总产量呈现为上升趋势，当边际产量为负值时，总产量一定呈下降趋势，而当边际产量的值为零时，总产量最大。

那这个和导数有什么关系呢？我们用脚都知道平均产量(AP)等于总产量除以工人人数，然而其在函数图像上是总产量函数上相应点与原点连线的斜率（斜率，表示一条直线相对于横坐标轴的倾斜程度。一条直线与某平面直角坐标系横坐标轴正半轴方向的夹角的正切值即该直线相对于该坐标系的斜率）。

以6个工人为例，平均产量是6.7个，6个人对应的总产量是总产量曲线上的B点，直线OB的斜率为6.7。7个工人时，平均产量为8.1个，对应总产量曲线上的A点，直线OA的斜率为8.1。最为重要的关系是，边际产量函数的值等于总产量函数相应点的切线的斜率。

7个工人工作时，其边际产量为17个，在函数示意图中即为总产量函数上点A的切线的斜率。“当当当~当~"，如果对高数还有那么点印象的话，有没有似曾相识的感觉？是的，主角终于出现了！是它是它就是它，函数在某一点的导数就是该函数所代表的曲线在这一点上的切线斜率。

在数学中，函数是分析世上万事万物“变化”的方法，而导数正是用来分析函数“变化”的工具。导数和微分都是从微观上研究函数，描述物质运动的工具。只不过导数描述的是函数变化的快慢，而微分描述的是函数变化的程度。

导数的实质是函数增量与自变量增量之比的极限，其几何意义为函数上点切线的斜率，而这就是我们刚刚所讨论“边际”概念的过程。

当我们粗略地知道“边际”的数学模型就是“导数”后，所有与边际相关的问题，都可以利用这一数学工具进行研究和解决。

有人说导数是“开启物理学的敲门砖”，足见其有多么的重要。其实不仅在物理学中，在很多领域它都是不可或缺的工具。

求导可以让我们知道曲线上某点的斜率，因此就比较容易推测出之后曲线的倾斜情况或走势。

在金融领域里，如果能巧妙地运用这一方法，就能预测未来的动向，比如股价的涨跌趋势。

而在计算机领域的应用大家就更为熟悉了，许多女孩子拍照时喜欢用的美颜，以及我们经常使用的PS等图像处理软件，导数就是在图像处理过程中用来查找边缘以及抠图的重要算法原理。

那么在经济学中，进行增量分析时，就可以用导数分析实际问题的动态变化，进而进行管理决策。比如使用边际成本来研究成本变化规律，配合边际收入就可以计算出边际利润，在决策时根据边际利润是否大于0来决定方案是否可行。

参考资料：

《管理经济学》（第4版修订版），【美】H·克雷格·彼得森（H. CraigPetersen）W·克里斯·刘易斯（W. Cris Lewis）著，吴德庆译校，中国人民大学出版社

《7天搞定微积分》，【日】石山平大上丈彦著，李巧丽译。文中最后截图来源于本书

《高等数学》（第五版），同济大学应用数学系主编，高等教育出版社

（以上内容仅代表作者本人观点）

文/MBA 2105班 魏晓磊

责编/宣传部 桑玉娇

主编/孙逊审核/沈家桓

点它，分享点赞在看都在这里